- 머신 러닝 알고리즘을 직관적으로 이해
- 판다스, 넘파이, 맥플롯립으로 데이터를 읽고 처리하고 시각화 하기
- 파이썬으로 선형 분류 알고리즘 구현하기
2.1. 인공 뉴런 : 초기 머신 러닝의 간단한 역사
초창기 머신러닝에서 AI를 설계하기 위한 생물학적 뇌가 동작하는 방식을 이해하려는 시도를 함.
맥컬록-피츠(MCP) 뉴런이라는 간소화된 뇌의 뉴런 개념을 발표, 신경 세포를 이진 출력을 내는 간단한 논리회로로 표현.
프랑크 로젠블라트의 MCP 뉴런 모델 기반 퍼셉트론 학습 개념 발표.
자동으로 최적의 가중치를 학습하는 알고리즘 제안.
2.1.1. 인공 뉴런의 수학적 정의
인공 뉴런의 아이디어를 두 개의 클래스 가 있는 이진 분류 작업으로 불 수 있음.
두 클래스는 간단하게 1(양성 클래스)과 -1(음성 클래스)로 나타냄.
입력 값 x와 이에 상응하는 가중치 벡터 w의 선형 조합으로 결정 함수(ϕ(z))를 정의.
최종 입력인 z는 z=w1+x1+…+wmxm.

특정 샘플 x(i)의 최종 입력이 사전에 정의된 임계 값 보다 크면 클래스 1로 예측, 그렇지 않으면 클래스 -1로 예측.
퍼셉트론 알고리즘에서 결정 함수 ϕ(·)는 단위 계단 함수(unit step function)를 변형한 것.
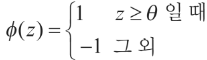
식을 간단히 하기 위해 임계 값 θ를 식의 왼쪽으로 옮겨, w0=-θ고 x0=1인 0번째 가중치를 정의. 이렇게 하면 z를 좀 더 간단하게 쓸 수 있음.

그리고 결정함수는 아래와 같이 됨.

아래의 그림이 퍼셉트론 결정 함수로 최종 입력 z = wTx가 이진 출력(-1 or 1)으로 압축 되는 방법과 이를 사용하여 선형 분리가 가능한 2개의 클래스 사이를 구별하는 방법을 보여줌.

2.1.2. 퍼셉트론 학습 규칙
퍼셉트론 모델 이면에 있는 전반적인 아이디어는 뇌의 뉴런 하나가 작동하는 방식을 흉내 내려는 환원주의(reductionism) 접근 방식을 사용하는 것. 즉, 출력을 내거나 내지 않는 2가지 경우만 있음.
초기 퍼셉트론 알고리즘 요약.
- 가중치를 0 또는 랜덤한 작은 값으로 초기화.
- 각 훈련 샘플 x(i)에서 다음 작업을 함.
- 출력 값 ŷ를 계산.
- 가중치를 업데이트.
출력 값은 앞서 정의한 단위 계단 함수로 예측한 클래스 레이블.
가중치 백터 w에 있는 개별 가중치 wj가 동시에 업데이트되는 것을 아래와 같이 쓸 수 있음.

가중치 wj를 업데이트하는 데 사용되는 Δwj 값은 퍼셉트론 학습 규칙에 따라 계산됨.

여기서 η는 학습률(learning rate). (일반적으로 0.0에서 1.0 사이 실수)
y(i)는 i번째 훈련 샘플의 진짜 클래스 레이블(true class label).
ŷ(i)는 예측 클래스 레이블(predicted class label)
가중치 벡터의 모든 가중치를 동시에 업데이트 한다는 점 이중요.
즉, 모든 가중치 Δwj를 업데이트하기 전에 ŷ(i)를 다시 계산하지 않음. 구체적으로 2차원 데이터셋에서는 다음과 같이 업데이트 됨.

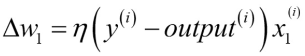

================================================================================
